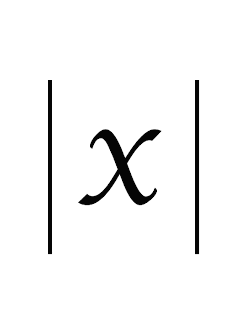Triangles are Hardly Square (1512)

In reviewing my information on triangles, I realized I had some trouble recalling the terminology of some of the angles. I decided to type some of the main ideas for my blog to help refresh my brain.

Most of us can probably recognize a 90-degree angle, otherwise called a right angle. This is where two perpendicular straight lines intersect. Corners of books, tables, chair legs, picture frames, appliances, and shoeboxes are all examples of right angles. For right triangles, they might not necessarily have the same length of sides.

Right Angle

The second type of angle I needed to review was the acute angle. I envision my kids saying “oh, isn’t that a cute little….(fill in the blank)” This helps me think of an acute angle as being something smaller. Smaller than what? An acute angle is smaller than a right 90-degree angle. This means that the acute angle must be within 0 and 90 degrees. This would be the equivalent of looking at a clock and the angle of the hands are between the 12, which is straight up and the 3 which is at 90-degrees going clockwise in the circle.

Acute Angle

The final type of angle I want to cover is the obtuse angle. When I think obtuse I somewhat correlate it with obese, which to me says “big”. It might not be the most politically correct way to think about it, but it works for me. An obtuse angle is one that measures between 90-degrees and 180-degrees. If we recall that 90-degrees is the edge where two perpendicular lines meet, greater than 90-degrees would be the space between that right angle and before you hit a half circle. So this would correlate to one clock hand being at 12, and the other between 3 and 6.

Obtuse Angle

Angles should not scare people when they start learning geometry. It is actually quite fun to solve the measures of an angle based on information about the others. Yes, I am a math geek!

Here is an alien angle game where you need to estimate how far to move the line to create the appropriate angle. Alien Angles Game

 

Patterns Are Pretty….Neat! (1510)

Do you ever find yourself doodling on a note pad, only to notice that you had made a pattern or picture without even realizing it? Patterns are present in many aspects of our lives. My daughter loves to draw and will make sure that her colors repeat exactly the same when she is creating certain projects.

This Spring I was able to teach my first lesson plan in my mentor’s kindergarten classroom. I had been in the classroom all year, which made it easier to interact with the students and know their capabilities. I planned with the teacher to do a lesson introducing the five senses, and I specifically focused on the sense of touch.  After reviewing and tweaking the plan I was finally ready to roll.

The project portion of the lesson was to integrate their sense of touch and different textures by creating a 3-pattern on a strip of paper. I had prepared small 1” pieces of sponge, bubble wrap, cotton balls, colored popsicle sticks, ribbon, felt fabric, scouring pad, buttons, and Easter grass. The students were to pick 3 textures and repeat them in a 5 x 17 strip of colored paper and be able to recite to an adult what their pattern was. Some of the students were struggling with the concept of this at first. The children were fully capable of patterning at this point of the year when they were using similar objects, for examples colored stickers or blocks. When I threw in the factor of different textures and sizes they couldn’t completely remember on their own what a 3 pattern was. The teacher was glad we did the project so she could revisit the topic that day, and then again before the end of the school year. It was fun to be part of the “ah-ha” moment she had with what her students were struggling with.

Once the students had set out their patterns, and before they glued, they were to raise their hand and have an adult review their work. I was very pleased when some of the students would use the texture words along with repeating the pattern. An example was my daughter saying, “Rough, smooth, soft, rough, smooth, soft.”

I look forward to introducing the concept of patterns to my class in the future. Ideas for the activities could be colored beads strung out to make a necklace, paper chains, stickers, blocks, crayons, and shapes. The possibilities are endless! If you relate the project with seasonal items the children might find it extra fun.

Here are two great websites that have interactive games and worksheets to use with students.
Pattern Worksheets

Pattern Mania

Here is my FAVORITE part of this blog! I finally got everything to work to record my screen as my daughter used the e-manipulative pattern game. She had so much fun helping me and showing off her skills! 

  

1st Pattern Recording with 6-year-old Abby

2nd Pattern Recording with 6-year-old Abby

Basic Addition – Kindergarten(1510)

When young children start their first day of school, they walk into the classroom having such a wide range of abilities. I look at the kids who have been in preschool for 1 or 2 years, some who have had daycare type exposure to learning, some have stay at home parents who have diligently worked on their ABC’s and 123’s. What about those children who have had little to no education before they strap on that backpack? Depending on where you live, you might see very little or quite diverse student capabilities.

I began volunteering in my daughter’s kindergarten classroom right away last fall after I was laid off. It was the best thing I could have ever asked for! I found so many valuable things in those short 9 months. In one small room I uncovered a love for teaching and being around children, a master teacher that my daughter learned so much from, and a woman who encouraged me to go back to school and who also agreed to be my mentor. Kindergarten is one of the most crucial grades in the school for so many reasons. When I was deciding what grades I wanted to focus on, I immediately knew the younger children was where I would be best suited. On the flip side, my heart races at the thought of having such a burden to teach a child how to read, write, behave in a school setting and respect themselves, their peers, and their teachers.

I want to discuss the basic addition that children learn in this magical first year of class. Once the number recognition and understanding was there for these students, they gradually worked into addition in the winter months. I remember sitting in the classroom observing a lesson and having my own “ah-ha” moment as I watched Mrs. Dunphy instruct the children. A very easy concept, when you have two numbers that you want to add together, you simply start with the largest number and then count up the amount of the next number.

For example, I have 3 apples and I need to add 2 more. I start at 3 and simply count up 2 places to 4, and 5 as the ending point. There are great hands-on manipulatives to help with the mathematical learning process. Unifex cubes, base blocks, paper chain links, checkers, or any other object can be used to show examples of addition. Children need to see things in different formats to help the concepts stay with them. It is beneficial to mix in lecture, worksheets, projects and stations for the students to reinforce their math skill. My mentor switched her math time from the afternoon to the morning half way through the year because the students were tuned in earlier in the day. She was very thoughtful with how she worked in simple math concepts of patterns, addition, and subtraction within some of their daily stations in addition to their set math lessons. She has learned over the years to keep it light and fun and the kids will stay engaged in the learning process.

Marble Math Addition

Basic Math Games 

In closing, I share a heartwarming example of how you can never give up on a child in your classroom. This year I knew all of the kids quite well and each of their abilities and some of the things they struggled with, or so I thought. I went over to a sweet little girl; I will call Susie, to check her off on her addition worksheet. Susie had struggled quite a bit with many concepts this first year, did not have much confidence, was shy and timid at times, and also has a heart of gold. I walked over to see the page of about 50 basic addition problems completely filled in. I sat down next to her on my own yellow stability ball and went through the whole sheet and couldn’t help buy start to smile. Susie had done EVERY PROBLEM RIGHT! I asked her if anyone helped her and how she did so well, to which she responded, “I don’t know, I just did my best work!” I gave her the biggest high five; great big hug and told her how proud I was of her for doing so well.

My eyes started to fill up with tears as I walked over to the teacher to show her the paper and explain the scenario. Mrs Dunphy responded with, “You can never give up on any child, because it is when you least expect it that the light bulb will go on and they will finally get it.” I know that these words will ring in my head in the years to come. There were many similar stories towards the end of the year in this classroom with certain students who didn’t know any letters or numbers in September and passed their grade equivalency tests in May.

Teachers do make a difference! I can’t wait to share my love of math and problem solving with the little ones who will make their way to my room. I hope someday to have these “magic skills” like Mrs. Dunphy. It is amazing to see the change that is possible in a child when you give them the love and attention they each deserve.

A Cup of This - A Dash of That (1512)

I love to cook and honestly can’t remember how young I was when I first entered the kitchen. I can tell you that once my mom and grandma taught me how to bake, and I could read a recipe, that I was the official baker in our household of 6. Needless to say, I ALWAYS had to double any cookie or brownie recipe, as it did not last long with 4 kids in the house.

Looking back, perhaps this is where my love of math came into play as well. My dad was, and still is, the “geek” and numbers man that helped me throughout school. He even gave me the gentle nudge to pursue my accounting degree the first time around in college. My mom was the busy housewife trying to make ends meet and keep us all happy around the dinner table.

In my eyes, a recipe is like a puzzle that must be put together “just so” in order to come out perfectly. I have learned through trial and error that baking needs more exact measurements, while other recipes for cooking you can become a little more creative and innovative.

A recipe is compiled of different measurements that have been tested by others to create something delicious. It will usually include measurements in terms of cups, teaspoons and tablespoons. This is where the fun of fractions comes into the picture! Here is a link that gives equivalent measurements to either reduce or enlarge a recipe.

Cooking Measurement Equivalents 

I recently ran into some confusion with my 83-year-old grandma. She makes WONDERFUL molasses cookies and I wanted to bake a large batch to hand out for teacher appreciation week for my kid’s teachers and teaching assistants. She emailed me two recipes, which confused me like crazy. I was trying to take the larger one and cut it in half to get the 2^nd recipe she had given me, however nothing was lining up. She wasn’t home to answer my question, but my sister finally responded that they were actually two separate recipes that she thought were both good and wanted to give me options. Uffda! And yes, I will share those great family secrets with you all here too!

Grandma Pearl's Cookies

Grandma Pearl's Large Batch of Cookies

Abby and Grandma Pearl 2009 Christmas Baking

Laura, Cousin Evan, and Grandma Pearl 2011 Christmas Baking

Absolutely Math is Fun! (1510)

The absolute value of an integer sparked my interest while I was recently reviewing my math homework. I remembered that it was something with an “easy” answer no matter what the problem was, but I couldn’t remember the exact definition of what it meant. The absolute value of a number is the distance it is away from zero. Whether the number is -6 or 6, you are still only 6 spaces away from zero. When you input a negative or a positive number (or zero), the end result will always be positive (or zero). The notation for writing absolute value uses two bars on each side of a number, not parenthesis.


For example:
|-5| = 5 and |5| = 5

This is read “the absolute value of the opposite of 5 equals 5” and “the absolute value of 5 equals 5”.

One thing to note when dealing with the absolute value is that the “-” or normally called negative sign, should be viewed as “the opposite of sign”, not necessarily a negative sign. The reason for this approach is that you can have an equation where you might have - |-x|. From everything I’ve discussed you might say “positive x” for the answer, however you have to look closely at where the bars are placed. Anything within the bars |-x| results in a positive x, however when you add the opposite sign outside of the bars, the ultimate answer is –x.

Absolute Value Number Ball Game

Calculating Area (1512)

I have really been hoping to replace the carpet in my basement for quite some time and I’m debating on spending the money now or not. What does this have to do with math you might ask? EVERYTHING! I have to take the materials and labor into account, along with my monthly family budget.

 

One option would be to replace only the spare bedroom; the other option would be to include the whole basement hallway, family room and bedroom. While trying to figure out if it was a justified expense I first need to calculate the area to be covered. The bedroom is rather small with a closet that should be included.

To determine the area of carpet needed, I first had to decide if my room was a square or rectangle to use the appropriate formulas. I quickly realized that the room is longer than it is wide just be estimation, so I concluded that this room is a rectangle.

The formula to find the area of a rectangle is: Area = length x width 

The formula to find the area of a square is: Area = s x s where s is the length of each side

The measurements of the room are 14 feet long x 12 feet wide = 168 square feet. I also need to have matching carpet in the closet as well or it wouldn’t look too good if we ever decide to sell. The closet is essentially another long skinny rectangle that is 12 feet long and 3 feet wide = 36 feet. The total area needed is 204 feet (36 feet for closet + 168 feet for the main bedroom). You can imagine this as needing 204 of those squares that are 12” x 12” and putting them end-to-end for the whole room. Of course there will need to be some cuts made when they put the closet portion in for the door, so there will be a waste factor that I will include about 10%, or another 20 square feet. The total square footage I would buy is 225.

I shopped around, and for a decent carpet pad underneath and the actual carpet, I’m looking at about $3.50 per square foot x 225 square feet = $787.50 for the entire bedroom. I have a friend who would install it with my husband so it would only cost me the food and beverage while he was there. I know that I could go a cheaper route and spend less on materials, but I’d rather buy something that will last. Unfortunately after doing all of the computations, I think I will just have to shut that bedroom door and pretend like it doesn’t bother me. I’m an unemployed non-traditional student who has a pretty strict budget right now. My accounting background tells me that I should focus my funds on paying off debt and creating a savings until I land that great elementary teaching position in another 3 years!

Here is a link to a website, Math is Fun, that can help with calculating the area of different objects.

I'm in My Prime, How About You? (1510)

Prime Numbers

This is one of those math topics that I honestly don’t use in my daily life, and have likewise forgotten the basics to what makes a number a prime number. I vaguely remembered that 5 and 7 were some of the first ones on the list, but I obviously needed a refresher when looking at the difference between a prime and composite number.

Here is a great interactive game that really gets the heart thumping and brain moving. Prime Shooter requires a person to have a quick reaction time. I found myself at the edge of my seat trying to shoot the prime numbers!

Dictionary.com defines our numbers as follows:

Prime number:

A positive integer that is not divisible without remainder by any integer except itself and 1, with 1 often excluded: For example, the integers 2, 3, 5, and 7 are prime numbers.

Composite Number:

A number that is a multiple of at least two numbers other than itself and 1.

To give a few examples of these types of numbers you can look at the list of numbers 2-10 as the number 1 is only divisible by itself.

2 - This is divisible only by the numbers 1 and 2, so it is a prime number

3 – This is divisible only by the numbers 1 and 3, so it is a prime number

4 – This is divisible by the numbers 1, 2, and 4 so it is a composite number

5 – This is divisible only by the numbers 1 and 5, so it is a prime number

6 – This is divisible by the numbers 1, 2, 3, and 6 so it is a composite number

7 – This is divisible only by the numbers 1 and 7, so it is a prime number

8 – This is divisible by the numbers 1, 2, 4, and 8 so it is a composite number

9 – This is divisible by the numbers 1, 3, and 9 so it is a composite number

10 – This is divisible by the numbers 1, 2, 5, and 10 so it is a composite number

Off of the top of my head, I use a shortcut to decide if a number is prime by seeing if it is an even number, which is obviously divisible by 2. I also think to myself on whether the number is easily divisible by 3, 5, and 7. (This obviously gets a little more difficult as the numbers get higher.) When your brain fails you, it is easy to do a quick search for a table online. I’m including a link that is helpful for this. 

Prime Numbers List

Don't be afraid of the math items that you haven't used for years. Embrace the challenge, do a little research and refresh that part of your brain!

Snowflakes, in July?? (1512)

Abby's first attempt

Abby's Snowflake

My 6 year old daughter asked for help to make snowflakes over the 4^th of July weekend when it was 90 degrees outside! We were on a camping trip and had a little downtime this past weekend, and my artistic daughter wanted to make something fun. We got out her paper and markers and decided to make some snowflakes. I started showing her how the paper needed to be folded from a square, then into a triangle and then another small triangle. She has made them before of course, but it seemed to be a good math lesson for this camping trip. My 4-year-old son was interested too, but he couldn’t quite get the cutting down for such a small area with his little fingers. The first attempt on her own ended up in a piece of paper crumbled into many pieces because she had cut through the edges too far. She soon got the hang of how deep she could cut in, which edges corresponded to the outside and which were the middle of the snowflake. The symmetry when it is done is what she loves the most! She practiced making tiny slits, diamonds, circles and even hearts while cutting through the layers.

Here is a quick video on tips to make the perfect snowflake.

It is never too early to introduce children to the names of shapes and where we find them in our every day life. There also has been many times where we are sitting down with the Magna Doodle and draw shapes and pictures. My son likes to say, “Build a house Mommy”! Obviously in our brains we usually start with the outside square or rectangle, then the triangle for a roof, then the square windows, rectangle vertical door, circle doorknob and any other details we might be imagining at the time. By introducing kids to these images early in life, it puts it in their head to be on the lookout for them. For instance, a sailboat on the lake looks like it has triangles that make up the sail reaching up high above the rest of the boat. If a teacher can get the kids involved with fun projects and they are much more willing to spend the time on learning about math!